Overview
Parks are important spaces for recreation and leisure in cities. Conventional metrics that measure the provision of parks to city residents usually summarise the park area within a given region (e.g. per capita park area). However, there is a need to characterise the wide variety of parks (e.g. nature areas, gardens, waterfront parks, outdoor playgrounds, etc.) that serve different groups of people. When planning at fine spatial scales, such metrics are also limited by their coarse spatial resolution and the presence of artificial boundaries.
The package home2park provides a way to measure multiple aspects of park provision to homes, at the resolution of individual buildings. The key features include the ability to:
- Download relevant data from OpenStreetMap (OSM) such as buildings, parks and features related to recreation. The user may also supply data for new buildings and parks, for the purpose of future scenario planning.
- Redistribute coarse-scale population data per census unit into residential buildings, also known as ‘dasymetric mapping’, which helps highlight specific areas where more people will benefit from the presence of parks.
- Summarise at each park multiple attributes that are important for recreation (e.g. dense vegetation, length of waterfronts, open spaces, trails, etc.).
- Calculate the supply (provision) of the park attributes to each residential building, while accounting for ‘distance decay’, or the fact that supply from parks further away are reduced.
Installation
Install the development version of home2park from GitHub:
devtools::install_github("ecological-cities/home2park", ref = "main")Setup
Load the package:
library(home2park)
#> Registered S3 methods overwritten by 'stars':
#> method from
#> st_bbox.SpatRaster sf
#> st_crs.SpatRaster sf1. Process city population
The first step is to process data related to the residential population (e.g. population census counts, residential buildings), in order to get the population count per building. The package comes with example data from the city of Singapore. This includes population counts per census unit in the years 2018 and 2020, and land use zones based on the Master Plan released in the years 2014 and 2019. To get the residential buildings for the population census conducted in 2020, we can download building polygons from OpenStreetMap on 2021-01-01, and subset them to areas within ‘residential’ land use zones in the 2019 Master Plan. The processed polygons can then be rasterised in preparation for dasymetric mapping.
data(pop_sgp) # population count per census unit (years 2018 & 2020)
pop_sgp <- sf::st_transform(pop_sgp, sf::st_crs(32648)) # transform to projected crs
# merge all census units for chosen year (2020) into single multi-polygon
# next function requires that polygons are merged
city_boundaries <- pop_sgp %>%
dplyr::filter(year == 2020) %>%
sf::st_union() %>%
sf::st_as_sf() %>%
smoothr::fill_holes(threshold = units::set_units(1, "km^2")) %>% # clean up
smoothr::drop_crumbs(threshold = units::set_units(1, "km^2")) %>%
sf::st_make_valid()
# get buildings from OpenStreetMap (use closest matching archive date)
# raw data saved in tempdir() unless otherwise specified
buildings <- get_buildings_osm(place = city_boundaries,
date = as.Date(c("2021-01-01"))) %>%
dplyr::mutate(year = 2020)
# rasterise population - specify relevant column names
pop_rasters <- rasterise_pop(pop_sgp,
census_block = "subzone_n",
pop_count = "pop_count",
year = "year")
# rasterise land use - specify relevant column names and residential land use classes
data(landuse_sgp)
landuse_sgp <- sf::st_transform(landuse_sgp, sf::st_crs(32648)) # transform to projected crs
landuse_rasters <- rasterise_landuse(landuse_sgp,
land_use = 'lu_desc',
subset = c('1' = 'RESIDENTIAL',
'2' = 'COMMERCIAL & RESIDENTIAL',
'3' = 'RESIDENTIAL WITH COMMERCIAL AT 1ST STOREY',
'4' = 'RESIDENTIAL / INSTITUTION'),
sf_pop = pop_sgp)
# rasterise buildings - specify relevant column names
# the column 'levels' is a proxy for how densely populated the building can be (i.e. more residents per unit area)
buildings_rasters <- rasterise_buildings(buildings,
proxy_pop_density = 'levels',
year = 'year',
sf_pop = pop_sgp,
sf_landuse = landuse_sgp)Next, perform dasymetric mapping to redistribute the population counts per census unit region (year 2020) into the residential buildings. The number of building ‘levels’ from OSM can be used as a proxy for population density (i.e. more residents per unit area).
# list element 2 is for the year 2020
popdens_raster <- pop_dasymap(pop_polygons = pop_rasters$pop_polygons[[2]],
pop_perblock_count = pop_rasters$pop_count[[2]],
pop_perblock_density = pop_rasters$pop_density[[2]],
land_relative_density = buildings_rasters[[2]])Here’s a screenshot showing an overlay of the multiple datasets used to redistribute the population data per census unit (subzones) across residential buildings.
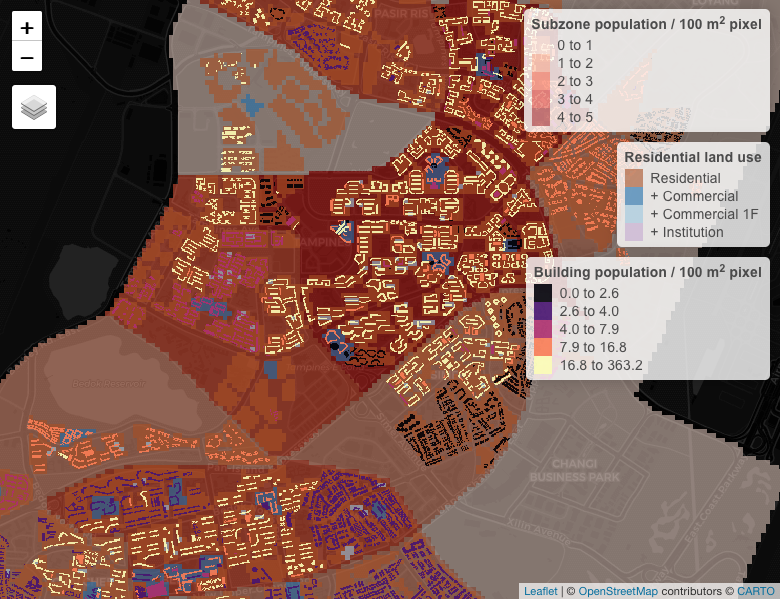
Example screenshot showing an overlay of multiple datasets used to redistribute the population across buildings within residential land use zones. The legends are ordered (top to bottom) by increasing spatial resolution.
Finally, we can convert this raster to building polygons each with a population count. Note that this is provided as an example dataset data(buildings_pop_sgp) in this package.
buildings_pop_sgp <- pop_density_polygonise(input_raster = popdens_raster)
head(buildings_pop_sgp)#> Simple feature collection with 6 features and 1 field
#> Geometry type: POLYGON
#> Dimension: XY
#> Bounding box: xmin: 371080.2 ymin: 143490 xmax: 377260.2 ymax: 157710
#> Projected CRS: WGS 84 / UTM zone 48N
#> popcount geometry
#> 1 32.367111 POLYGON ((371080.2 157060, ...
#> 2 20.880897 POLYGON ((375490.2 145930, ...
#> 3 2.311594 POLYGON ((373650.2 145960, ...
#> 4 56.747406 POLYGON ((372100.2 144130, ...
#> 5 6.368404 POLYGON ((372240.2 157710, ...
#> 6 9.502521 POLYGON ((377240.2 143520, ...2. Process parks
The example dataset data(parks_sgp) contains parks in Singapore and selected attributes related to recreation/leisure (downloaded from OSM on 2021-01-01). This was downloaded and processed as follows. Parks within other cities (provided polygon boundaries) can be downloaded and processed in a similar manner.
# get park polygons
parks_sgp <- get_parks_osm(city_boundaries,
date = as.Date(c("2021-01-01")))
# get playground points
playgrounds <- get_playgrounds_osm(place = city_boundaries,
date = as.Date(c("2021-01-01")))
# get trail lines
trails <- get_trails_osm(place = city_boundaries,
date = as.Date(c("2021-01-01")))
# convert to lists
point_list <- list(playgrounds) # calculation of attributes requires input to be named list
names(point_list) <- c("playground")
line_list <- list(trails)
names(line_list) <- c("trails")
# per park, calculate point count/density & line length/ratio
parks_sgp <- parks_calc_attributes(parks = parks_sgp,
data_points = point_list,
data_lines = line_list,
relative = TRUE)
head(parks_sgp[, 28:33]) # view park attributes#> Simple feature collection with 6 features and 6 fields
#> Geometry type: MULTIPOLYGON
#> Dimension: XY
#> Bounding box: xmin: 364364.4 ymin: 138034.6 xmax: 374328.5 ymax: 142157.4
#> Projected CRS: WGS 84 / UTM zone 48N
#> area perimeter playground_count playground_ptdensity
#> 1 2454.365 [m^2] 346.5265 [m] 0 0 [1/m^2]
#> 2 1964.286 [m^2] 305.3844 [m] 0 0 [1/m^2]
#> 3 219319.203 [m^2] 3019.2241 [m] 0 0 [1/m^2]
#> 4 22513.834 [m^2] 615.1039 [m] 0 0 [1/m^2]
#> 5 571259.766 [m^2] 3973.5567 [m] 0 0 [1/m^2]
#> 6 67533.345 [m^2] 1092.2758 [m] 0 0 [1/m^2]
#> trails_length trails_length_perim_ratio geometry
#> 1 0.0000 [m] 0.0000000 [1] MULTIPOLYGON (((371727.8 13...
#> 2 0.0000 [m] 0.0000000 [1] MULTIPOLYGON (((371454.2 13...
#> 3 4072.5481 [m] 1.3488724 [1] MULTIPOLYGON (((367154.1 13...
#> 4 837.9212 [m] 1.3622434 [1] MULTIPOLYGON (((369087 1409...
#> 5 20947.6579 [m] 5.2717652 [1] MULTIPOLYGON (((373309.8 14...
#> 6 905.5080 [m] 0.8290105 [1] MULTIPOLYGON (((364400.3 14...3. Recreation supply
The processed data can now be used to calculate the provision of park attributes per residential building. The total supply \(S\) of each park attribute to a building is calculated based on the following equation. Its value depends on the distances between that particular building and all parks; supply from parks further away are generally reduced as a result of the negative exponential function e-cd, an effect also known as the ‘distance decay’ (Rossi et al., 2015).
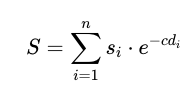
where
\(S\) = Total supply of a specific park attribute to the building from parks \(i\); \(i\) = 1,2,3, … \(n\) where \(n\) = total number of parks citywide.
\(s_{i}\) = Supply of a specific park attribute from park \(i\). A perfect positive linear association is assumed, since the focus is on supply metrics.
\(d_{i}\) = Distance in kilometres from the building to park \(i\) (e.g. Euclidean, Manhattan, etc.).
\(c\) = Coefficient determining rate of decay in supply \(s_{i}\) with increasing distance.
The value of coefficient \(c\) depends on both park and park visitors’ attributes, such as socio-demographic factors and preferences for activities that may impel shorter or longer travel (Rossi et al., 2015). For example, (non-Euclidean) distance decay in the ratio of visitors at urban parks in Beijing in Tu et al. (2020) fit the negative exponential curve e-cd, with coefficient \(c\) empirically determined as 0.302. Empirical cut-off distances were 1–2km where most (> 50%) people would visit a park and 5–10km beyond which few (< 5%) people would visit a park.
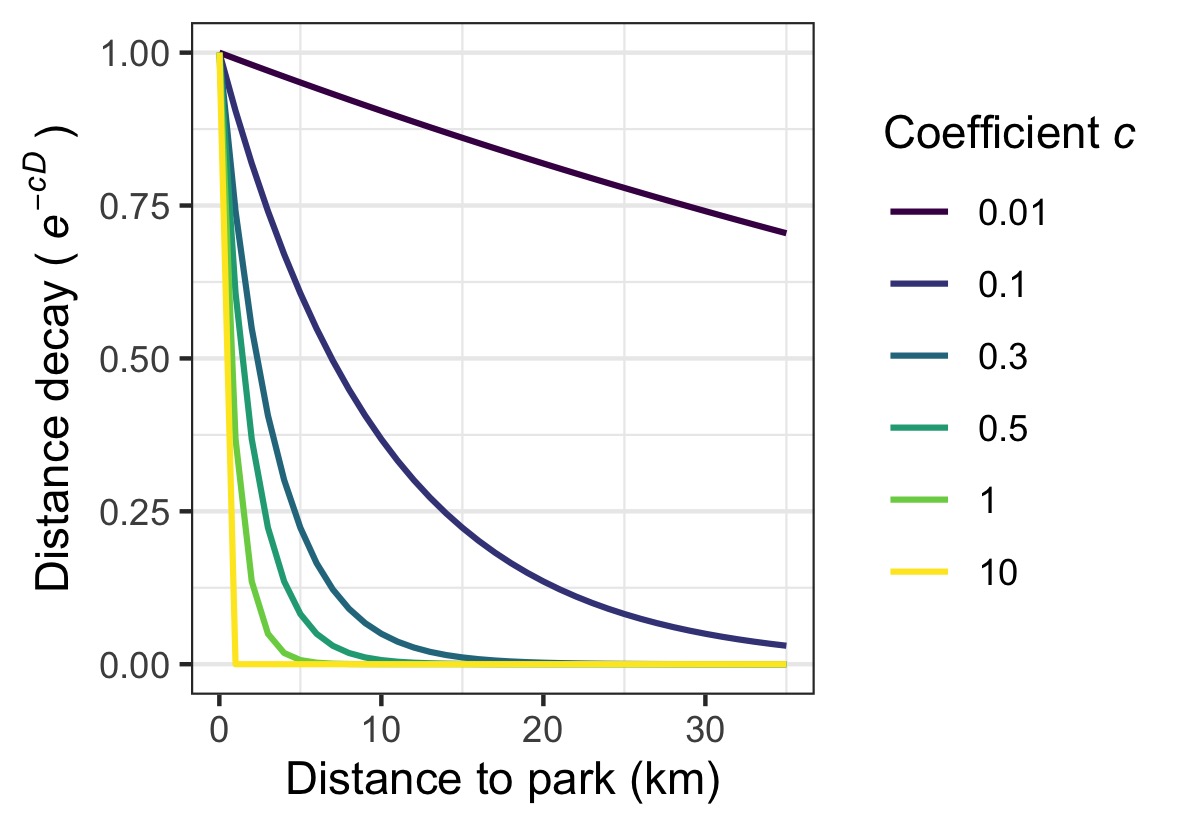
Figure: The value of Coefficient c and its effect on the distance decay between a building and park.
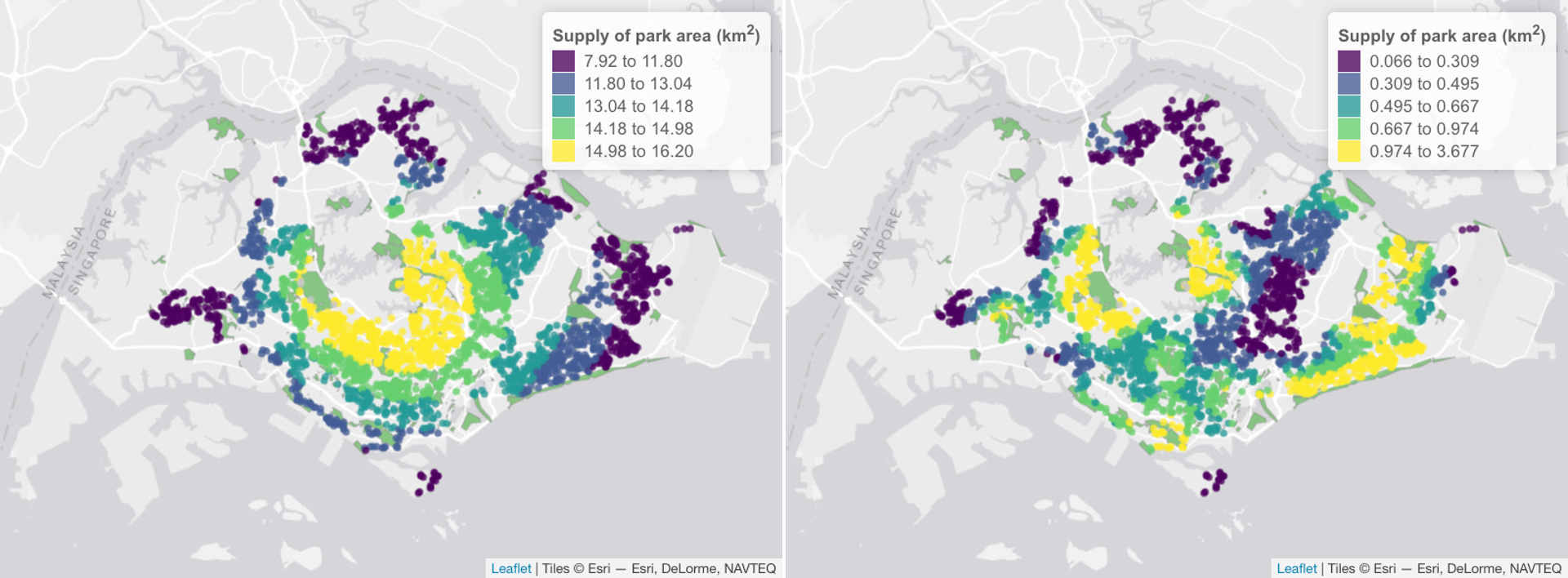
Screenshot: Examples showing the supply of OSM park area to residential buildings in Singapore for the year 2020 when the value of Coefficient c is 0.1 (left panel) and 1 (right panel). Each building is denoted as a pount (a random subset is shown). The color palette for the buildings (points) is binned according to the quantile values.
To calculate the supply of each park attribute, we first calculate the pairwise distances between all buildings and parks (a distance matrix). This output is supplied to the function recre_supply(). For example, we can calculate the supply of park area to each building. This supply value can then be multiplied by the population count per building, to obtain the total supply to all residents. This can help highlight important areas where more people would benefit from the presence of parks.
# convert buildings to points (centroids), then calculate distances to every park
m_dist <- buildings_pop_sgp %>%
sf::st_centroid() %>%
sf::st_distance(parks_sgp) %>% # euclidean distance
units::set_units(NULL)
m_dist <- m_dist / 1000 # convert distances to km
# new column for the supply of park area
buildings_pop_sgp$area_supply <- recre_supply(park_attribute = parks_sgp$area,
dist_matrix = m_dist,
c = 0.302) # e.g. from Tu et al. (2020)
# supply to all residents per building
buildings_pop_sgp$area_supplytopop <- buildings_pop_sgp$area_supply * buildings_pop_sgp$popcountWe can visualise the supply of park area to building residents using library(tmap):
# convert buildings to points (centroids) for plotting
buildings_pop_sgp <- buildings_pop_sgp %>%
sf::st_centroid() %>%
dplyr::mutate(across(everything(), as.vector)) %>% # remove attributes from columns for plotting
dplyr::mutate(across(.cols = contains("area"), # convert from m2 to km2
.fns = function(x) x*1e-6))
tmap::tmap_mode("view")
tmap::tm_basemap("Esri.WorldGrayCanvas") +
tmap::tm_shape(parks_sgp) +
tmap::tm_polygons(col = "#33a02c",
alpha = 0.6,
border.col = "grey50",
border.alpha = 0.5) +
tmap::tm_shape(buildings_pop_sgp) +
tmap::tm_dots(title = "Supply of park area (km<sup>2</sup>)",
col = "area_supplytopop",
border.col = "transparent",
palette = viridis::viridis(5),
style = "quantile",
size = 0.01,
alpha = 0.7,
showNA = FALSE)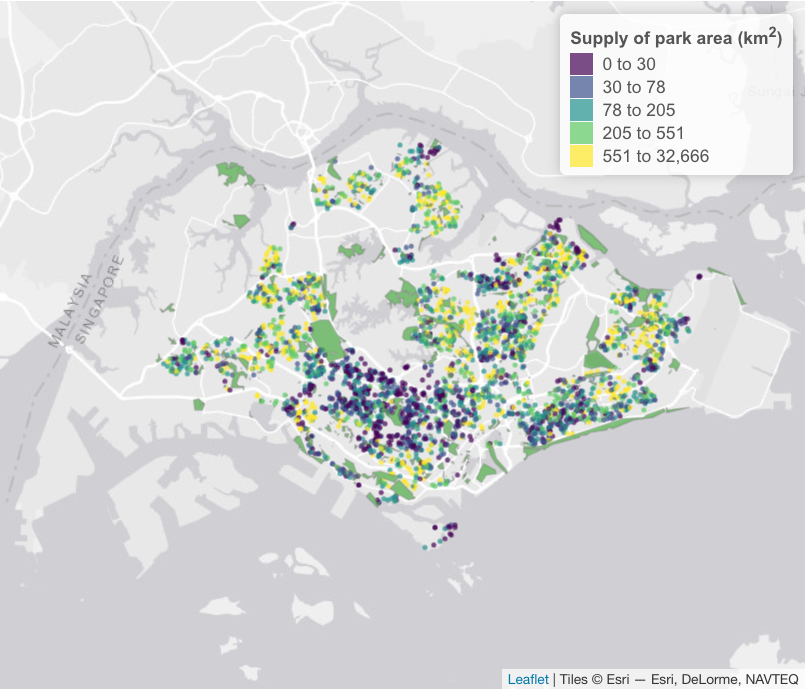
Screenshot: Supply of park area to building residents in Singapore based on OSM data (2020). Each building is denoted as a point (a random subset is shown). The color palette is binned according to the quantile values.
Finally, it is also possible to summarise the supply values of buildings within coarser spatial regions. This allows us to compare our results with conventional park provision metrics (per capita park area) for the selected year 2020.
Calculate summary statistics (e.g. sum, median, mean) for the supply of park area within each region:
# append subzone info to buildings if building intersects with subzone
buildings_subzones <- buildings_pop_sgp %>%
sf::st_join(pop_2020,
join = sf::st_intersects,
left = TRUE) %>%
sf::st_set_geometry(NULL)
# summarise total/median/average supply value for all buildings within subzone
buildings_subzones <- buildings_subzones %>%
dplyr::group_by(subzone_n) %>%
dplyr::summarise(across(.cols = c(area_supply, area_supplytopop),
.fns = sum, .names = "{.col}_sum"),
across(.cols = c(area_supply, area_supplytopop),
.fns = median, .names = "{.col}_median"),
across(.cols = c(area_supply, area_supplytopop),
.fns = mean, .names = "{.col}_mean"))
# join information to pop_2020, calculate supply per capita
pop_2020 <- pop_2020 %>%
dplyr::left_join(buildings_subzones) %>%
dplyr::mutate(area_supplyperpop = area_supplytopop_sum / pop_count * 1e-6) %>% # convert to km2
dplyr::mutate(area_supplyperpop = ifelse(is.infinite(area_supplyperpop), NA, area_supplyperpop)) # make infinite NACalculate the (conventional) per capita park area for each census unit:
subzones_parks <- sf::st_intersection(pop_2020, parks_sgp) # subset census unit polygons to those that intersect parks, append park info
subzones_parks$parkarea_m2 <- sf::st_area(subzones_parks) # calc area of each polygon
# calculate total park area per census unit
subzones_parks <- subzones_parks %>%
dplyr::group_by(subzone_n) %>%
dplyr::summarise(parkarea_m2 = as.numeric(sum(parkarea_m2))) %>%
sf::st_drop_geometry()
# join information to pop_2020, calculate park area per capita
pop_2020 <- pop_2020 %>%
dplyr::left_join(subzones_parks) %>%
dplyr::mutate(parkarea_m2 = ifelse(is.na(parkarea_m2), 0, parkarea_m2)) %>% # make NA 0
dplyr::mutate(parkperpop_m2 = parkarea_m2 / pop_count * 1e-6) %>% # convert to km2
dplyr::mutate(parkperpop_m2 = ifelse(is.infinite(parkperpop_m2), # make infinite NA
NA, parkperpop_m2)) %>%
dplyr::mutate(parkperpop_m2 = ifelse(is.nan(parkperpop_m2), # make NaN NA
NA, parkperpop_m2))Similarly, we can visualise the park metrics summarised per region:
tmap::tm_basemap("Esri.WorldGrayCanvas") +
tmap::tm_shape(pop_2020) +
tmap::tm_polygons(title = "Park area per capita (km<sup>2</sup>)",
group = "Subzones: Per capita park area (conventional)",
col = "parkperpop_m2",
palette = "Greens", alpha = 0.7,
style = "quantile",
border.col = "white", border.alpha = 0.5, lwd = 1) +
tmap::tm_shape(pop_2020) +
tmap::tm_polygons(title = "Supply of park area per capita (km<sup>2</sup>)",
group = "Subzones: Per capita supply of park area",
col = "area_supplyperpop",
palette = "Greens", alpha = 0.7,
style = "quantile",
border.col = "white", border.alpha = 0.5, lwd = 1)The following figure provides a visual comparison between the provision of park area per capita summarised per region (subzone), based on conventional metrics (left panel) and derived from each residential building (right panel). The interactive map is viewable online at https://ecological-cities.github.io/home2park/articles/online/metric-comparisons.html.
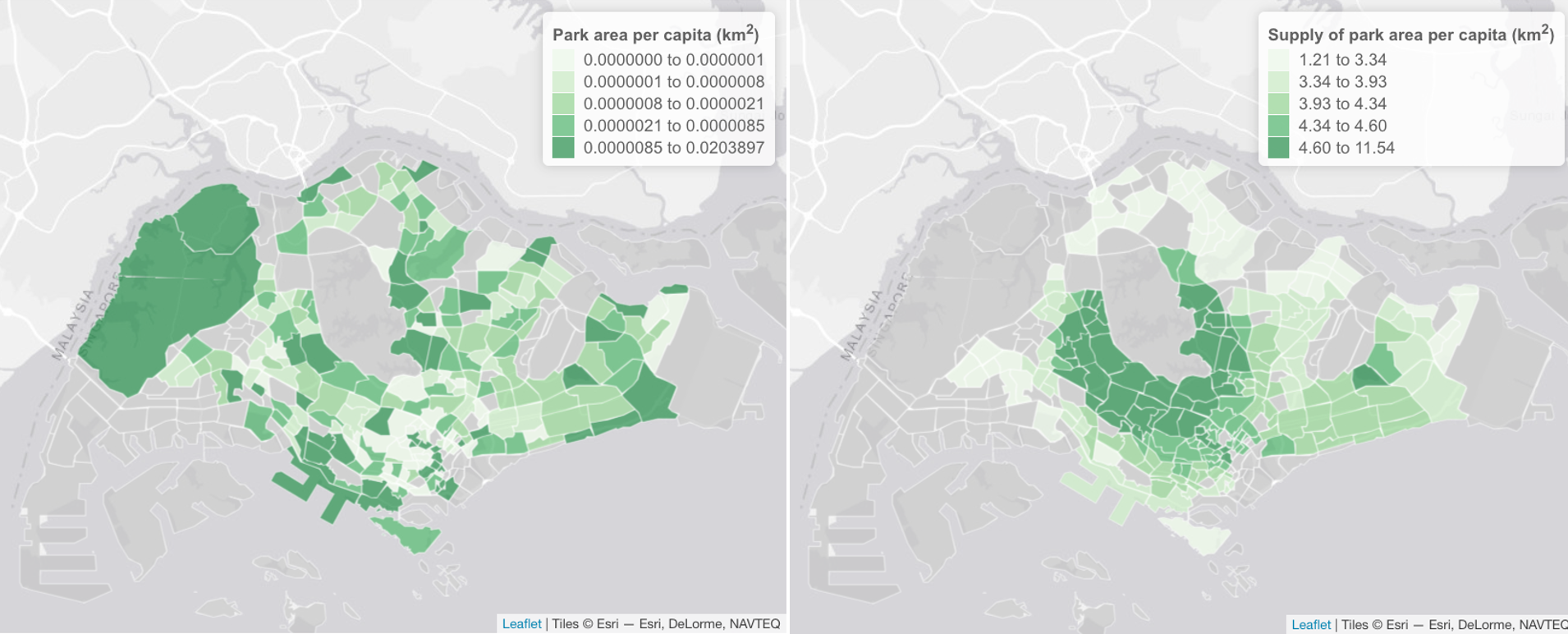
Screenshot: Provision of park area per capita within each subzone in Singapore, as measured by the total park area per subzone (left panel); and by the supply of park area to residents within residential buildings (right panel). Based on OSM data (2020). For the calculation of the supply value per building, the value for Coefficient c was set at 0.302. The color palettes are binned according to quantile values.
Data sources
Singapore census data from the Department of Statistics Singapore. Released under the terms of the Singapore Open Data Licence version 1.0.
Singapore subzone polygons from the Singapore Master Plan Subzones. Released under the terms of the Singapore Open Data Licence version 1.0.
Singapore Master Plan Land Use Zones for the years 2014 and 2019. Released under the terms of the Singapore Open Data License.
Building polygons derived from map data copyrighted OpenStreetMap contributors and available from https://www.openstreetmap.org. Released under the terms of the ODbL License.
Park polygons and summarised attributes (trails, playgrounds) derived from map data copyrighted OpenStreetMap contributors and available from https://www.openstreetmap.org. Released under the terms of the ODbL License.
References
Rossi, S. D., Byrne, J. A., & Pickering, C. M. (2015). The role of distance in peri-urban national park use: Who visits them and how far do they travel?. Applied Geography, 63, 77-88.
Tu, X., Huang, G., Wu, J., & Guo, X. (2020). How do travel distance and park size influence urban park visits?. Urban Forestry & Urban Greening, 52, 126689.